Mastering Sliding Window —— Patterns, Tricks, and Real LeetCode Examples
A concise guide to sliding window techniques — fixed and variable size windows, key patterns, and common tricks for solving array and substring problems in O(n).
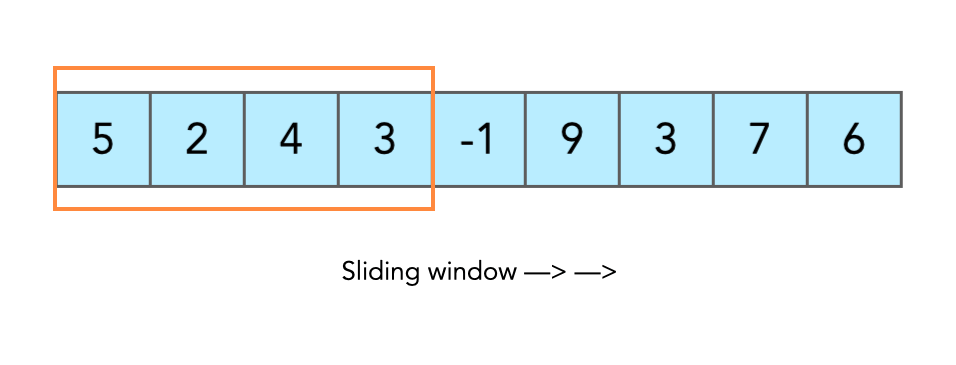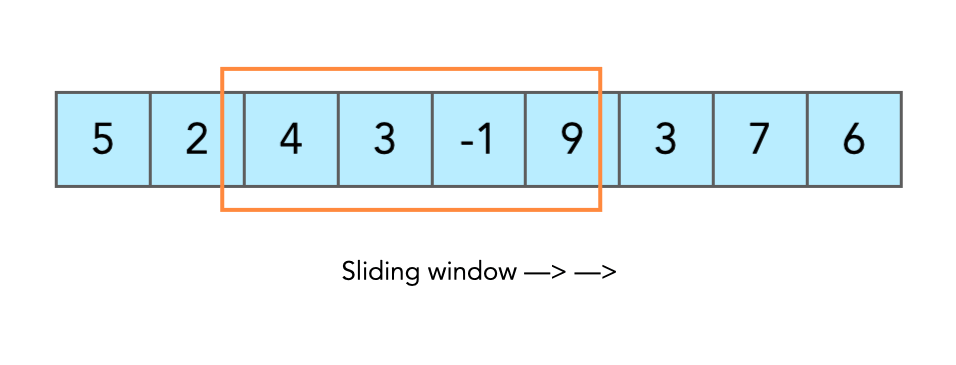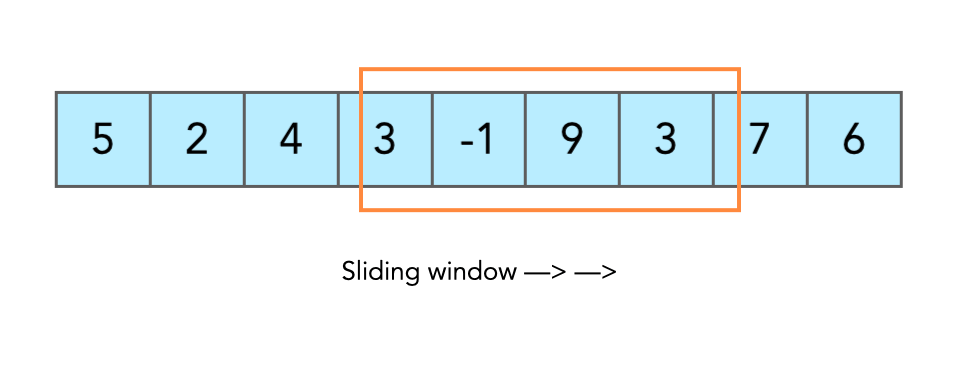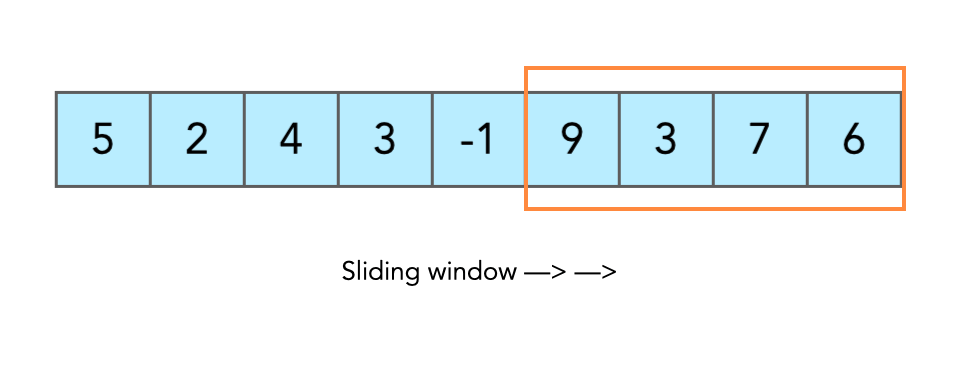
滑动窗口(Sliding Window)是数组和字符串题目中的常用技巧,几乎是刷题必备。它的核心思想是维护一个动态区间,通过左右指针的移动实现对子数组/子串的快速处理。相比暴力枚举所有区间,滑动窗口通常能把时间复杂度优化到 O(n)。
一、定长滑动窗口
窗口大小固定为 k,移动过程中只需维护这段区间的统计信息:
思路:
入窗:右边移入一个元素,更新统计信息(元素和、平均数、计数等)。若当前窗口长度不足
k,重复入窗操作更新:判断当前统计信息是否满足条件,用 O(1) 时间更新答案。
出窗:左边移出一个元素,再次更新统计信息。
以上三步适用于所有定长滑窗题目。
应用:
最大/最小和、平均数、计数(元音、黑块、distinct 数字等)。
判断是否存在某种模式(子串/子数组哈希、异位词检测)。
固定窗口内的最优值问题(最大和、最少操作数、最多种类等)。
对于一些较为复杂的问题,需要用到一些数据结构或技巧维护统计信息:
哈希/字典计数:维护窗口中元素频率。
单调队列:维护区间最大/最小值。
双指针 + 计数器:在固定长度基础上,扩展到模式匹配类问题。
例题1:1423. 可获得的最大点数
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
参考思路 来源:灵茶山艾府
拿走 k 张,剩下 n−k 张。这里 n 是 cardPoints 的长度。
由于拿走的点数和 + 剩下的点数和 = 所有点数和 = 常数,所以为了最大化拿走的点数和,应当最小化剩下的点数和。
由于只能从开头或末尾拿牌,所以最后剩下的牌必然是连续的。
至此,问题变成:
- 计算长为
n−k的连续子数组和的最小值。
这可以用定长滑动窗口解决。
设
m=n−k,计算第一个长为m的子数组元素和,即s=cardPoints[0]+cardPoints[1]+⋯+cardPoints[m−1]。初始化minS=s。计算下一个子数组的元素和,即
s′=cardPoints[1]+cardPoints[2]+⋯+cardPoints[m]。由于s′−s=cardPoints[m]−cardPoints[0],所以只需要把s增加cardPoints[m]−cardPoints[0],就可以 O(1) 算出下一个子数组的元素和。依照这个方法,从
i=m开始向后枚举,每次把s增加cardPoints[i]−cardPoints[i−m],然后用s更新minS的最小值。最后,用
cardPoints的元素和,减去minS,就得到了答案。
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
int maxScore(vector<int>& cardPoints, int k) {
int n = cardPoints.size();
int m = n - k;
int s = reduce(cardPoints.begin(), cardPoints.begin() + m);
int min_s = s;
for (int i = m; i < n; i++) {
s += cardPoints[i] - cardPoints[i - m];
min_s = min(min_s, s);
}
return reduce(cardPoints.begin(), cardPoints.end()) - min_s;
}
};
二、不定长滑动窗口
窗口大小不固定,通过双指针(left/right)动态调整,常见于“满足/不满足某条件”。
注:滑动窗口相当于在维护一个队列。右指针的移动可以视作入队,左指针的移动可以视作出队
2.1 越短越合法 → 求最长/最大
思路:条件限制“越短越容易满足”,所以窗口要尽量扩展。
右指针不断扩展窗口;
当条件不合法时,移动左指针缩小窗口;
过程中维护最大窗口长度。
应用:
无重复字符最长子串;
至多 k 种字符/元素;
连续子数组最大和/最大长度;
允许一定次数修改/删除的最长子数组。
2.2 越长越合法 → 求最短/最小
思路:条件限制“越长越容易满足”,所以窗口要尽量收缩。
右指针不断扩展窗口;
当条件合法时,尝试收缩左指针;
过程中维护最小窗口长度。
应用:
子数组和 ≥ target 的最短长度;
最小覆盖子串;
最小区间问题。
例题2:1658. 将 x 减到 0 的最小操作数
给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。
如果可以将 x 恰好 减到 0 ,返回 最小操作数 ;否则,返回 -1 。
参考思路 来源:灵茶山艾府
移除的是 nums 最左边或最右边的元素,那么剩下的元素是什么?是 nums 的连续子数组。
移除的元素和 x + 剩余的元素和 = nums 的所有元素之和 s。
所以剩余的元素和 = s−x。
问题变成:
- 从
nums中找最长的子数组(这样移除的数尽量少),满足子数组的元素和恰好等于s−x。
最后答案为 nums 的长度减去最长子数组的长度。
子数组的长度可以是 0,所以下面代码初始化
ans=−1。如果初始化ans=0,就无法区分是否真的存在符合要求的子数组。
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
int minOperations(vector<int>& nums, int x) {
int target = reduce(nums.begin(), nums.end()) - x;
if (target < 0) {
return -1; // 全部移除也无法满足要求
}
int ans = -1, left = 0, sum = 0, n = nums.size();
for (int right = 0; right < n; right++) {
sum += nums[right];
while (sum > target) {
sum -= nums[left];
left++; // 缩小子数组长度
}
if (sum == target) {
ans = max(ans, right - left + 1);
}
}
return ans < 0 ? -1 : n - ans;
}
};
2.3 求子数组个数
技巧在于 计数方式。
2.3.1 越短越合法
当窗口 [left, right] 合法时,说明 [left, right], [left+1, right], …, [right, right] 全部合法。
增加 right - left + 1 个答案。
2.3.2 越长越合法
当窗口 [left, right] 不合法时,最后一次合法是 [0..left-1, right]。
增加 left个答案。
2.3.3 恰好型
转换成两个“至少/至多”问题:
例如:count(和 ≥ k) - count(和 ≥ k+1)。
或者 count(和 ≤ k) - count(和 ≤ k-1)。
可以写成通用 solve(limit) 函数,然后调用两次求差。
应用:
统计和 < k / 和 = k 的子数组数;
统计包含某些字符/条件的子串数。
例题3:2537. 统计好子数组的数目
给你一个整数数组 nums 和一个整数 k ,请你返回 nums 中 好 子数组的数目。
一个子数组 arr 如果有 至少 k 对下标 (i, j) 满足 i < j 且 arr[i] == arr[j] ,那么称它是一个 好 子数组。
子数组 是原数组中一段连续 非空 的元素序列。
参考思路 来源:灵茶山艾府
核心思路:
如果窗口中有 c 个元素 x,再进来一个 x,会新增 c 个相等数对。
如果窗口中有 c 个元素 x,再去掉一个 x,会减少 c−1 个相等数对。
用一个哈希表 cnt 维护子数组(窗口)中的每个元素的出现次数,以及相同数对的个数 pairs。
外层循环:从小到大枚举子数组右端点 right。现在准备把 x=nums[right] 移入窗口,那么窗口中有 cnt[x] 个数和 x 相同,所以 pairs 会增加 cnt[x]。然后把 cnt[x] 加一。
内层循环:如果发现 pairs≥k,说明子数组符合要求,右移左端点 left,先把 cnt[nums[left]] 减少一,然后把 pairs 减少 cnt[nums[left]]。
内层循环结束后,[left,right] 这个子数组是不满足题目要求的,但在退出循环之前的最后一轮循环,[left−1,right] 是满足题目要求的。由于子数组越长,越能满足题目要求,所以除了 [left−1,right],还有 [left−2,right],[left−3,right],…,[0,right] 都是满足要求的。
也就是说,当右端点固定在 right 时,左端点在 0,1,2,…,left−1 的所有子数组都是满足要求的,这一共有 left 个。
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
long long countGood(vector<int>& nums, int k) {
long long ans = 0;
unordered_map<int, int> cnt;
int pairs = 0, left = 0;
for (int x : nums) {
pairs += cnt[x]++;
while (pairs >= k) {
pairs -= --cnt[nums[left]];
left++;
}
ans += left;
}
return ans;
}
};
例题4:992. K 个不同整数的子数组
给定一个正整数数组 nums和一个整数 k,返回 nums 中 「好子数组」 的数目。
如果 nums 的某个子数组中不同整数的个数恰好为 k,则称 nums 的这个连续、不一定不同的子数组为 「好子数组 」。
- 例如,
[1,2,3,1,2]中有3个不同的整数:1,2,以及3。
子数组 是数组的 连续 部分。
参考思路 来源:寂
我们要求的是恰好有 k 个不同整数的子数组数量。
先思考:如果能快速求出「至多 k 个不同整数」的子数组数量,再减去「至多 k−1 个不同整数」的子数组数量,得到的就是「恰好 k 个不同整数」的子数组数量。
所以问题变成:
- 如何用滑动窗口求出「至多
k个不同整数」的子数组数量?
具体做法:
用一个哈希表(或数组)统计窗口内的整数出现次数。
右指针
r向右扩展,如果新元素第一次出现,就让不同整数数目 +1。当不同整数超过
k时,移动左指针 l 缩小窗口,直到窗口合法。当窗口合法时,以
r结尾的所有子数组[l, r], [l+1, r], ..., [r, r]都满足条件,一共有r−l+1个。
最后:
记 f(k) 表示「至多 k 个不同整数」的子数组数量,答案就是 f(k) − f(k−1)。
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
int subarraysWithKDistinct(vector<int>& nums, int k) {
return f(nums, k) - f(nums, k - 1);
}
private:
int f(vector<int>& nums, int k) {
int n = nums.size();
int cnt[20001] = {0};
int collect = 0;
int ans = 0;
for (int l = 0, r = 0; r < n; r++) {
if (cnt[nums[r]]++ == 0) {
collect++;
}
while (collect > k) {
if (--cnt[nums[l++]] == 0) {
collect--;
}
}
ans += r - l + 1;
}
return ans;
}
};
三、解题时的核心思路
识别题型:
窗口大小固定?→ 定长滑窗。
窗口大小不固定?→ 不定长滑窗。
判断条件单调性:
越短越容易满足 → 求最长;
越长越容易满足 → 求最短;
子数组个数问题 → 看能否转化成单调性 + 计数。
实现技巧:
哈希表/数组计数频率;
单调队列优化最大/最小;
差分技巧(恰好型 = 至少型差分)。
👉 总结一句话:
滑动窗口的本质是维护一个动态区间,利用条件的单调性来缩放窗口,实现 O(n) 的扫描。